【LeetCode】剑指Offer——树

7（105）重建二叉树

示例 1:

给定两个整数数组 $preorder$ 和 $inorder$ ，其中 $preorder$ 是二叉树的先序遍历， $inorder$ 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• $1 <= preorder.length <= 3000$
• $inorder.length == preorder.length$
• $-3000 <= preorder[i], inorder[i] <= 3000$
• $preorder$ 和 $inorder$ 均 无重复 元素
• $inorder$ 均出现在 $preorder$
• $preorder$ 保证 为二叉树的前序遍历序列
• $inorder$ 保证 为二叉树的中序遍历序列

题解

class Solution {
public:
    unordered_map<int, int> map;
    TreeNode* build(vector<int>& preorder, vector<int>& inorder,int pre_root, 
    int inorder_left,int inorder_right){
        if(inorder_left > inorder_right)
            return NULL;
        TreeNode* root = new TreeNode(preorder[pre_root]);
        
        // 根节点在中序序列中位置，划分左右子树边界
        int inorder_root = map[preorder[pre_root]];
        // 左子树前序中根节点的位置在，pre_root+1，左子树在中序中边界，[inorder_left,inorder_root-1]
        root->left = build(preorder,inorder,pre_root+1,inorder_left,inorder_root-1);
        // 右子树在前序中的根节点位于：根节点+左子树长度+1 即 pre_root+inorder_root-inorder_left+1
        // 右子树在中序中的边界：[inorder_root+1,inorder_right]
        root->right = build(preorder,inorder,pre_root+inorder_root-inorder_left+1,inorder_root+1,inorder_right);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        // 中序序列用于查找根节点
        for(int i=0;i< inorder.size();i++)
        {
            map[inorder[i]] = i;
        }
        return build(preorder,inorder,0,0,inorder.size()-1);
    }
};

26 树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

$ 3 / \ 4 5 / \ 1 2$
给定的树 B：

$ 4 / 1$
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

限制：

0 <= 节点个数 <= 10000

题解

class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        return (A != NULL && B!=NULL )&&(recur(A,B)||isSubStructure(A->left,B)||isSubStructure(A->right,B));
    }
    bool recur(TreeNode *A, TreeNode *B){
        if(B==NULL)return true;
        if(A==NULL|| A->val !=B->val)return false;
        return recur(A->left,B->left)&&recur(A->right,B->right);
    }
};

27（226） 二叉树的镜像

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

$ 4 / \ 2 7 / \ / \ 1 3 6 9$
镜像输出：

   4   /  \  7   2 / \  / \ 9  6 3  1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

题解

/*226*/
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)return nullptr;
        TreeNode *tmp = root->left;
        root->left = invertTree(root->right);
        root->right = invertTree(tmp);
        return root;
    }
};

/*027*/
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==NULL)return NULL;
        stack<TreeNode*> stack;
        stack.push(root);
        while(!stack.empty())
        {
            TreeNode* node = stack.top();
            stack.pop();
            if(node->left!=NULL)stack.push(node->left);
            if(node->right!=NULL)stack.push(node->right);
            TreeNode *tmp = node->left;
            node->left = node->right;
            node->right = tmp;
        }
        return root;
    }
};

28（101）对称二叉树

给你一个二叉树的根节点 $root$ ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 $[1, 1000]$ 内
• $-100 <= Node.val <= 100$

题解

/*101*/
class Solution {
public:
    bool check(TreeNode *p, TreeNode *q)
    {
        if(!p && !q)return true;
        if(!p || !q)return false;
        return p->val == q->val && check(p->left,q->right) && check(p->right, q->left);
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

/*028*/
class Solution {
public:
    bool check(TreeNode *u, TreeNode *v) {
        queue <TreeNode*> q;
        q.push(u); q.push(v);
        while (!q.empty()) {
            u = q.front(); q.pop();
            v = q.front(); q.pop();
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;

            q.push(u->left); 
            q.push(v->right);

            q.push(u->right); 
            q.push(v->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

32 - I 从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: $[3,9,20,null,null,15,7]$,

    3
   / \
  9  20
    /  \
   15   7

返回：

[3,9,20,15,7]

提示：

1. $节点总数 <= 1000$

题解

class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        if(root == NULL)return {};
        queue<TreeNode*> queue;
        vector<int> res;
        queue.push(root);
        while(!queue.empty()){
            TreeNode *node = queue.front();
            queue.pop();
            res.push_back(node->val);
            if(node->left != NULL)queue.push(node->left);
            if(node->right != NULL)queue.push(node->right);
        }
        return res;
    }
};

32 - II（102） 从上到下打印二叉树

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: $[3,9,20,null,null,15,7]$,

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

提示：

1. $节点总数 <= 1000$

题解

/*106*/
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> tnQueue;
        vector<vector<int>> res;
        if(root!=nullptr)tnQueue.push(root);
        while(!tnQueue.empty())
        {
            vector<int> tmp;
            for(int i= tnQueue.size();i>0;i--)
            {
                TreeNode* node = tnQueue.front();
                tnQueue.pop();
                tmp.push_back(node->val);
                if(node->left)tnQueue.push(node->left);
                if(node->right)tnQueue.push(node->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

32 - III 从上到下打印二叉树

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: $[3,9,20,null,null,15,7]$,

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [20,9],
  [15,7]
]

提示：

1. $节点总数 <= 1000$

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
    queue<TreeNode*> tnQueue;
        vector<vector<int>> res;
        if(root!=nullptr)tnQueue.push(root);
        while(!tnQueue.empty())
        {
            vector<int> tmp;
            for(int i= tnQueue.size();i>0;i--)
            {
                TreeNode* node = tnQueue.front();
                tnQueue.pop();
                if(res.size()%2==0)tmp.push_back(node->val);
                else tmp.insert(tmp.begin(),node->val);
                if(node->left)tnQueue.push(node->left);
                if(node->right)tnQueue.push(node->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

33 二叉搜索树的后序遍历序列

入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 $true$，否则返回 $false$。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

     5
    / \
   2   6
  / \
 1   3

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

提示：

1. $数组长度 <= 1000$

题解

class Solution {
public:
    bool recur(vector<int> postorder, int i,int j){
        if(i>=j)return true;
        int p=i;
        while(postorder[p]<postorder[j])p++;
        int m=p;
        while(postorder[p]>postorder[j])p++;
        return p==j && recur(postorder,i,m-1) && recur(postorder,m,j-1);
    }
    bool verifyPostorder(vector<int>& postorder) {
        return recur(postorder,0,postorder.size()-1);
    }
};

/*构建验证*/
class Solution {
public:
    int isEnd;
    void build(vector<int> postorder, int min, int max)
    {
        if(isEnd < 0)return;
        int vRoot = postorder[isEnd];
        if(vRoot>=max||vRoot<=min)return;
        isEnd--;
        build(postorder,vRoot,max);
        build(postorder,min,vRoot);
    }
    bool verifyPostorder(vector<int>& postorder) {
        if(postorder.empty()||postorder.size()==1)return true;
        isEnd=postorder.size()-1;
        build(postorder, INT_MIN,INT_MAX);
        return isEnd < 0;
    }
};

34（113） 二叉树中和为某一值的路径

给你二叉树的根节点 $root$ 和一个整数目标和 $targetSum$ ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

• 树中节点总数在范围 $[0, 5000]$ 内
• $-1000 <= Node.val <= 1000$
• $-1000 <= targetSum <= 1000$

题解

/*113*/
class Solution {
    vector<vector<int>> res;
    vector<int> path;
    void recur(TreeNode *root, int target){
        if(root==nullptr)return;
        path.push_back(root->val);
        target-= root->val;
        if(target==0 && root->left==nullptr && root->right==nullptr){
            res.push_back(path);
        }
        recur(root->left, target);
        recur(root->right, target);
        path.pop_back();
    }

public:
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        recur(root, targetSum);
        return res;
    }
};

36二叉搜索树与双向链表

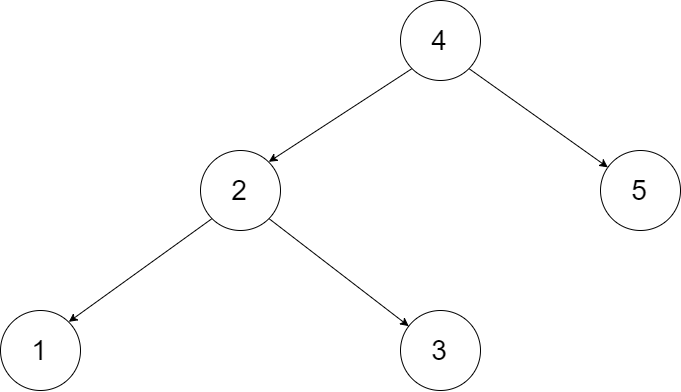
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

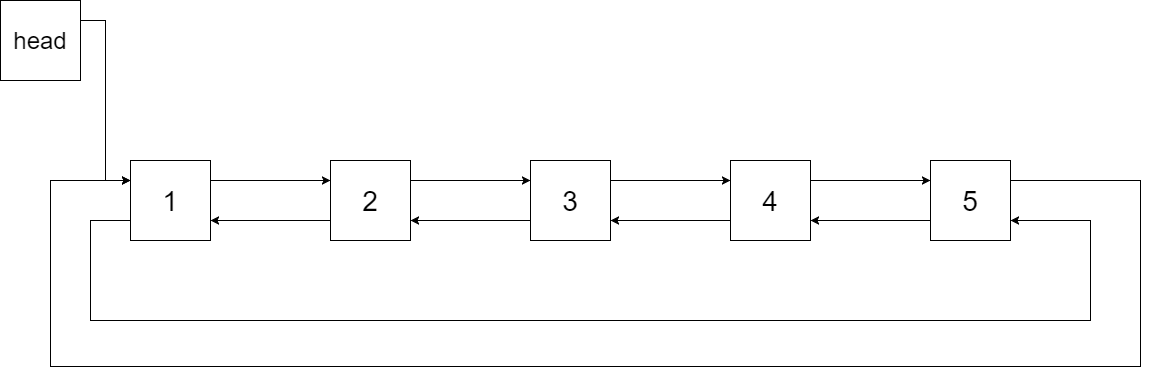
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

题解

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if(root==NULL)return NULL;
        dfs(root);
        head->left=pre;
        pre->right=head;
        return head;
    }
private:
    Node *pre, *head;
    void dfs(Node *cur){
        if(cur==NULL)return;
        dfs(cur->left);
        if(pre!=NULL)
            pre->right=cur;
        else
            head=cur;
        cur->left = pre;
        pre=cur;
        dfs(cur->right);
    }
};

37 序列化二叉树

题解

/*
 * @lc app=leetcode.cn id=297 lang=cpp
 *
 * [297] 二叉树的序列化与反序列化
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string ans;
        //层序遍历
        queue<TreeNode*> node_queue;
        node_queue.push(root);
        while(!node_queue.empty()){
            root=node_queue.front();
            if(root){
                ans+=to_string(root->val);
                node_queue.push(root->left);
                node_queue.push(root->right);
            }else ans+="null";
            ans.push_back(',');
            node_queue.pop();
        }
        cout<<ans<<endl;
        return ans;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        if(data=="null,")
            return nullptr;
        string tep_string;
        TreeNode dummyHeadNode,*dummyHead=&dummyHeadNode;
        queue<TreeNode**> node_queue;
        node_queue.push(&(dummyHead->left));
        for(char ch:data){
            if(ch==','){
                TreeNode** cur_node_pointer=node_queue.front();
                node_queue.pop();
                if(tep_string=="null")
                    *cur_node_pointer=nullptr;
                else{
                    *cur_node_pointer=new TreeNode(stoi(tep_string));
                    node_queue.push(&((*cur_node_pointer)->left));
                    node_queue.push(&((*cur_node_pointer)->right));
                }
                tep_string.clear();
            }else tep_string.push_back(ch);
        }
        return dummyHead->left;
    }

    
};



// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));
// @lc code=end

54 二叉搜索树的第k大节点

给定一棵二叉搜索树，请找出其中第 $k$ 大的节点的值。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

限制：

• 1 ≤ k ≤ 二叉搜索树元素个数

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int res, k;
    void dfs(TreeNode* root){
        if(root==NULL)return;
        dfs(root->right);
        if(k==0)return;
        if(--k==0)res=root->val;
        dfs(root->left);
    }
    int kthLargest(TreeNode* root, int k) {
        this->k=k;
        dfs(root);
        return res;
    }
};

55 - I（104） 二叉树的深度

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 $[3,9,20,null,null,15,7]$，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

提示：

1. $节点总数 <= 10000$

题解

/*DFS*/
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==nullptr)return 0;
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

/*BFS*/
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==NULL)return 0;
        queue<TreeNode*> q;
        q.push(root);
        int res=0;
        while(!q.empty()){
            for(int i = q.size();i;i--){
                auto node = q.front();
                q.pop();
                if(node->left)q.push(node->left);
                if(node->right)q.push(node->right);
            }
            res++;
        }
        return res;
    }
};

55 - II（110） 平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 $[3,9,20,null,null,15,7]$

    3
   / \
  9  20
    /  \
   15   7

返回 $true$ 。

示例 2:

给定二叉树 $[1,2,2,3,3,null,null,4,4]$

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4

返回 $false$ 。

限制：

• $0 <= 树的结点个数 <= 10000$

题解

/*055*/
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int recur(TreeNode* root){
        if(root==nullptr)return 0;
        int left = recur(root->left);
        if(left==-1)return -1;
        int right = recur(root->right);
        if(right == -1)return -1;
        return abs(left-right)<2 ? max(left,right) +1 : -1;
    }
    bool isBalanced(TreeNode* root) {
        return recur(root) != -1;
    }
};

/*110*/
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root==NULL)return true;
        return abs(depth(root->left)-depth(root->right))<=1 && isBalanced(root->left) && isBalanced(root->right);
    }

    int depth(TreeNode* root){
        if(root==nullptr)return 0;
        return max(depth(root->left),depth(root->right))+1;
    }
};

68 - I（235） 二叉搜索树（两个节点）的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root->val < p->val && root->val < q->val)
            return lowestCommonAncestor(root->right, p, q);
        if(root->val > p->val && root->val > q->val)
            return lowestCommonAncestor(root->left, p, q);
        return root;
    }
};

/*235*/
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(p->val > q->val){// 保证 p->val < q->val
            TreeNode *tmp = p;
            p=q;
            q=tmp;
        }
        while(root)
        {
            if(root->val < p->val)//p,q 在 root 右子树
                root = root->right;//遍历至右子节点
            else if(root->val > q->val)//p,q 在 root 左子树
                root = root->left;//遍历至左子节点
            else break;
        }
        return root;
    }
};

68 - II（236） 二叉搜索树（两个节点）的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 $[2, 105]$ 内。
• $-109 <= Node.val <= 109$
• 所有 $Node.val$ $互不相同$ 。
• $p != q$
• $p$ 和 $q$ 均存在于给定的二叉树中。

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr || root==p || root==q)return root;
        TreeNode *left=lowestCommonAncestor(root->left,p,q);
        TreeNode *right=lowestCommonAncestor(root->right,p,q);

        if(!left)return right;
        else if(!right)return left;
        else return root;
    }
};